Application of the Gradient Descent Method for Optimization of Spin System Parameters of Metabolite Molecules by NMR Spectra

Spectral form analysis

This work was conducted using equipment from the MIPT Shared Facilities Center. NMR spectra were acquired using a Varian Inova 500 NMR-spectrometer with a ¹H Larmor frequency of 500 MHz. All experiments were conducted in liquid solutions, and the spin Hamiltonian of the molecule in this case can be represented as [24-27]:

H = H_Z + H_J, (1)

where the first term represents the Zeeman interaction with the local magnetic field, while the second term represents the spin-spin J-coupling interaction:

$Hz={\displaystyle \sum _K v_k{S}_z^{(k)}},\text{ (2)}$

$H_{\text{J}}=\frac{1}{2}{\displaystyle \sum }_{k,l}{J}_{kl}\left(S_x^{(k)}{S}_x^{(l)}+S_y^{(k)}{S}_y^{(l)}+S_z^{(k)}{S}_z^{(l)}\right)\text{ (3)}$

Here, νk is the k-th spin precession frequency, and Jkl are J-coupling constants, which determine an interaction between the k-th and l-th spins. The precession frequency of the nuclear spin is determined as νk = γB₀(1 − σk), where γ is the gyromagnetic ratio, B₀ is the external magnetic field, and σk is the so-called shielding constant. Both resonant frequencies νk and coupling constants Jkl are the main characteristics of any molecule in NMR measurements and allow us to identify a specific molecule in a sample. One can consider the case of “weak” J-coupling between k-th and l-th nuclear spins: Jkl << |νk − νl|, when the corresponding part of the Hamiltonian can be reduced to the secular part: $H_J^{(k,l)}\approx J_{k,l}{S}_z^{(k)}{S}_z^{(l)}$ . Then the required calculations are simplified. However, for the case when Jkl is comparable to or greater than the chemical shift values difference |νk − νl|, which is also called “strong” coupling, it is necessary to consider the full contribution to the spin-spin interaction Hamiltonian without neglecting the non-secular part. Since “strong” coupling can be observed for some metabolites, we solved the optimization problem in a general way using a full form of Hamiltonian 3. Thus, the proposed algorithm does not rely on perturbation theory and considers “strong” spin-spin coupling (more general case), which makes computational methods more stable and allows us to successfully find parameters for, for example, AB systems.

Further, the corresponding matrix of the complete Hamiltonian (1) will be written in the basis of eigenstates of the Hamiltonian (2), that is, in the so-called computational basis. The eigenvalues of this matrix give us the energy levels of the nuclear spin system and, accordingly, the NMR spectrum, which depends on both chemical shifts and coupling constants. A comparison of the experimentally measured and calculated spectra gives us the opportunity to identify the corresponding molecule in the sample. In the following, the Hamiltonian matrix will be called the spin matrix.

All the necessary parameters of the spin matrices of molecules can be determined in experiments with pure samples, but in the studied samples containing both different concentrations of the molecules of interest and mixtures of molecules, these parameters may differ. Thus, we need to propose an efficient algorithm that modifies the parameters of the known spin matrix of a molecule in order to identify it from the observed NMR spectrum in the sample.

When creating the algorithm, it is necessary to take into account that the molecules interact with the environment, which leads to a broadening of the ideal lines of the observed spectra. In liquids, this broadening can be well described by the shape of Lorentz lines [28,29], which corresponds to the exponential relaxation law. In our model, we will use the law of exponential relaxation, which determines for each central line of the spectrum the corresponding width and shape of the line. We can represent the transformation of the observed NMR signal into the corresponding spectrum using the following relations:

$M(t)\propto e^{-\left(w-i{v}_0\right)t}\theta (t)\stackrel{ℱ}{\to }\frac{w}{w^2+{\left(v-v_0\right)}^2}+i\frac{v-v_0}{w^2+{\left(v-v_0\right)}^{\text{'}}}\text{ (4)}$

where M(t) is the experimentally observed signal, w is the peak width (relaxation rate), and ν, ν0 – spin resonant frequency with and without shielding, θ(t) is the Heaviside function, F is the Fourier transform operation,, which allows for shifting from the time-domain signal (FID) to the frequency-domain (spectrum). Therefore, the Lorentz peak model is used to generate the spectrum, and we, together with the parameters of the spin Hamiltonian, also train the relaxation coefficients.

For the universality of the model, we will train chemical shifts δ rather than resonant frequencies ν, which are field dependent:

$\delta =\frac{v-v_{\text{TMS}}}{v_0}\text{*}{10}^6\text{ (5)}$

where νTMS is the resonant frequency for tetramethylsilane.

When acquiring NMR spectra, a large number of scans are usually accumulated and averaged. To speed up the registration of spectra, the time between scans is usually set to about 3-6 s. For some nuclei of a molecule, this time may be insufficient for complete longitudinal relaxation, which may lead to a decrease in the intensity of the signal of this nucleus in the averaged NMR spectrum. To account for this factor, we introduced the parameter r affecting the intensity of peaks.

Thus, it is easy to see that in order to solve the problem, we need to find the following optimal parameters and values: chemical shifts, the matrix of J-coupling constants, relaxation rates that determine the width of the lines, as well as parameters for correcting the intensity of the lines.

Model architecture

The optimization algorithm is organized as follows: it receives a spectrum, which is represented by the y-axis coordinates of a graph, as input. The goal is to find the optimal model parameters in order to generate a synthesized graph that most closely resembles the original spectrum being processed. For these reasons, it is convenient to represent the frequencies of the spectrum, relaxation rates, and correction parameters as the corresponding vectors $\overrightarrow{\delta },\overrightarrow{w}$ and $\overrightarrow{r}$ . The model will predict a set of system parameters $\overrightarrow{\delta },\overrightarrow{w},\overrightarrow{r}$ and a matrix of coupling constants J using the experimental spectrum as input data.

In terms of meaning, it can be divided into two modules: internal and external. At the internal level, the model will build a synthetic spectrum from the current values of the system parameters. In turn, at the outer level, the model performs gradient optimization of the system parameters by comparing the experimental data (input) with the synthetic spectrum obtained from the inner level. In our work, we will apply the optimization algorithm only to data from ¹H spectra. But algorithm principles can be easily applied to study isotope spectra with other resonant frequencies, for example, ¹⁹F or ¹³C.

To build synthetic spectra for given parameters, we calculate the Hamiltonian of the system, determine its eigenvalues, select possible transitions using selection rules, and construct overall spectra by superimposing Lorentzian broadening on corresponding frequencies.

Optimization challenges

The model is implemented using the PyTorch machine learning framework for the Python programming language. This design ensures that the entire model is fully differentiable, allowing end-to-end optimization via gradient descent. The integration of physics-based computations (e.g., Hamiltonian construction and eigendecomposition) with conventional deep learning techniques facilitates the accurate simulation of complex spectral patterns, while also enabling parameter optimization based on experimental data.

To formulate an optimization problem for our model, we chose a loss function in the form

$\text{Loss}=\text{log}\left(2-\text{cos}\left(y_{sim },y_{exp }\right)\right),\text{ cos}\left(y_{sim },y_{exp }\right)=\frac{y_{sim }\cdot y_{exp }}{\left|\right|y_{sim }\left|\right|\cdot \left|\right|y_{exp }\left|\right|\text{'}}\text{ (6)}$

which is often used to process the Fourier spectra of various signals. Here, ysim, yexp — graphs of the corresponding synthetic (generated) and experimental (ground truth) spectra. This loss function was chosen for optimization because of the following reasons. First, in NMR spectroscopy, spectra are often processed in the frequency domain (Fourier space), where the norm of the vector corresponds to the intensity of the radiation. Cosine similarity measures the angle between spectral vectors in a multidimensional space, which physically corresponds to the degree of spectral similarity, regardless of the absolute amplitude, which depends on the strong magnetic field magnitude used for measurement. Second, the logarithmic transformation serves to numerically stabilize and prevent getting stuck in deep local minima (as discussed in the context of Figure 1). Finally, in the loss function (6) shift by 2 is due to the numerical stability of calculations. Generally, we do not know of a generally accepted loss function for solving such problems. Of course, it is possible to use other loss functions, for example, Mean Squared Error (MSE), Mean Absolute Error (MAE), or something else, but this requires a separate study and is already of special interest for research in the field of neural networks. General principles of hyperparameter selection for gradient optimization can be found in machine learning works [31-33].

Figure 1: In the left picture optimization algorithm becomes trapped in a local minimum due to the merging of the right peak of the blue doublet with the left peak of the red doublet. In the right picture, we use line broadening to avoid being trapped in local minima.

To evaluate the quality of the chosen parameters, we will utilize IoU (Intersection-over-Union) as a metric because of its favorable interpretability. It can be perceived as the ratio of the intersection area to the area of the union of the experimental graph and the graph drawn by our model. In the context of the identification of metabolites, this corresponds to the criterion: “what proportion of the informative spectral region coincides between the two spectra”. Also, this metric has invariant properties to baseline shifts and uneven amplitude changes. Note that experimental spectra are subject to measurement errors, which lead to underestimated results when using this metric.

The optimization problem arises due to narrow peaks, when incorrectly selected initial parameters can lead to a significant mismatch between experimental and generated peaks. For example, if the right peak of one doublet merges with the left peak of another, as shown in Figure 1, the optimization algorithm may fall into the trap of a local minimum. To solve this problem, we broadened the peaks of the experimental spectrum using convolution with a Lorentzian kernel.

Although the suggested gradient descent method does not offer a ready-made universal methodology, it can be used to optimize the parameters of spin systems instead of manually selecting parameters. Initial conditions of estimated values (chemical shifts, spin-spin interaction constants) are selected manually or from known sources [18](for example, GISSMO [18]). In the future, the parameters are optimized using the gradient descent method using a given loss function. After reaching the minimum of the loss function, a visual comparison of the model spectrum is performed, and the IoU is calculated to evaluate the optimization quality.

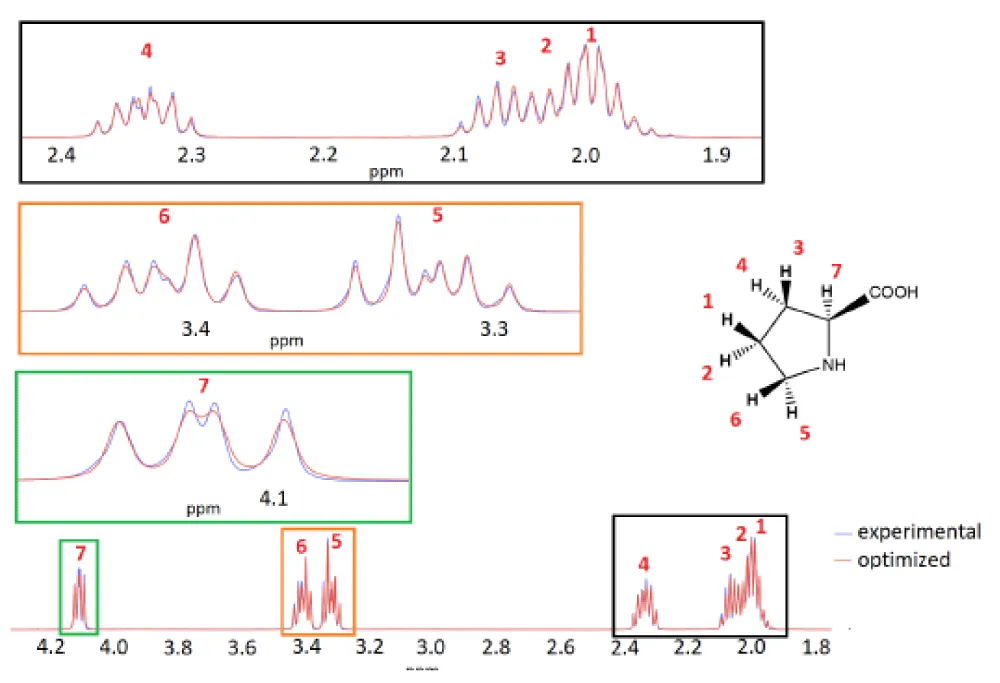
To illustrate the effectiveness of the model, we used the L-proline molecule as an example. The structure and ¹H NMR spectrum of the L-proline molecule are shown in Figure 2. ¹H NMR spectrum of L-proline contains signals from seven non-equivalent 1H nuclei. Most nuclei couple with several other nuclei at once, making the spectrum quite complex.

Figure 2: The structure of L-proline, experimental 1H NMR spectrum acquired at 500 MHz (blue) and calculated for optimized spin-system parameters [2] 1H NMR spectrum of L-proline (red). Here, the averaged matrix J was used.

To a first approximation, the J-coupling constants do not depend on the external magnetic field, but under certain conditions, they may depend on pH and temperature. Most of the system parameters ( $\overrightarrow{\delta },\overrightarrow{w},\overrightarrow{r}$ ) can vary depending on external factors such as pH, temperature, the strength, or inhomogeneity of the magnetic field [23]. At the same time, we will assume that the J-coupling parameters should not change significantly.

We will use the spin matrix provided by the ChenomX library for proline to find out if the parameters of our spin system can be improved. To do this, we will keep a fixed spin-spin coupling matrix J and try to optimize the remaining parameters by changing only the values of chemical shift δ and peak width w. Similarly, let’s look at optimization with additional fixed parameters of the effective peak intensity coefficient r and a system in which we optimize all parameters. We will evaluate the quality using the indicator we entered.

To assess the validity of such an assumption, five different L-proline spectra were analyzed:

1. Spectrum acquired at 500 MHz on our spectrometer. The sample was dissolved in D2O, and a single-pulse pulse sequence was applied;
2. Spectrum acquired at 500 MHz on our spectrometer. The sample was dissolved in phosphate buffer solution with pH 7.4, and a CPMG pulse sequence was applied.
3. Spectrum acquired at 500 MHz obtained from the GISSMO open library.
4. Spectrum acquired at 600 MHz obtained from the GISSMO open library.
5. Spectrum acquired at 600 MHz obtained from the HMDB open library.

Due to the complexity of the task and the presence of noise in the real spectra, the models converge to slightly different spin matrices. Therefore, to get an approximate matrix, we use matrix averaging over all models. The average matrix is shown in Figure 3.

Figure 3: The averaged matrix J obtained for five different L-proline NMR spectra.

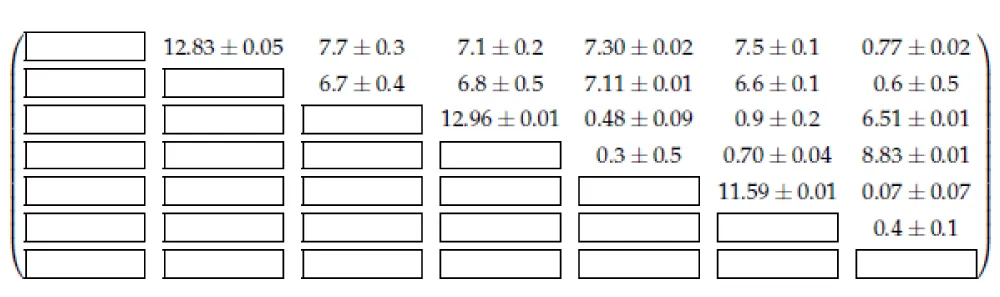
The IoU metrics obtained for the average J matrix are shown in Table 1, where the second column is responsible for the metrics with our average spin matrix. For a more precise verification of the dependence of the matrix J on the external parameters of the experiment, it is necessary to conduct a separate study; however, the data presented in the table indicate that this assumption is valid for the studied spectra.

Using our model and average matrix J, we have successfully optimized spin-system parameters for L-proline (Table 2 and Figure 2). To estimate the computational time required for the proposed method, optimization runs were performed on a laptop equipped with an NVIDIA GeForce GTX 1650 (mobile) graphics processing unit (GPU) and an Intel Core i5-10300H central processing unit (CPU) with 4 cores and 8 threads, and a base frequency of 2.5 GHz. The estimated computational time is about 10 minutes. The Adam, standard optimization algorithm, was used with a learning rate parameter configured at approximately 10⁻². Furthermore, a ReduceLROnPlateau learning rate scheduler was implemented, which was parameterized with a factor of 0.9 to dynamically adjust the learning rate during the training process. In specific cases, the Lorentz expansion method was applied, typically utilizing values within the range of 1 to 10, in order to improve the robustness and stability of the optimization procedure. The code and associated data used in this study are openly available in the GitHub repository.

The article [30] presents the matrix J for the proline molecule obtained by annealing. Table 1: Calculated IoU for the full optimized spectrum and fixed averaged J matrix of the spin system for five different experimental spectra of L-proline algorhythm. In addition, another matrix J is available in the ChenomX application. To compare the matrices J from the above matrix sources with the matrix obtained using our algorithm, an optimization of the parameters of the spin system ( $\overrightarrow{\delta },\overrightarrow{w}$ ) of proline was performed with a fixed matrix J obtained from each source of proline and all values r = 1.

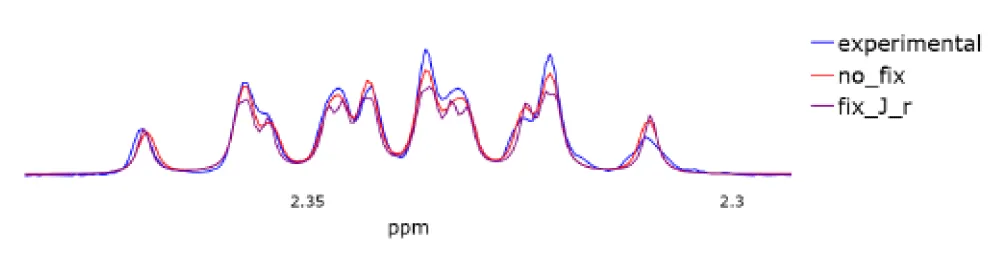
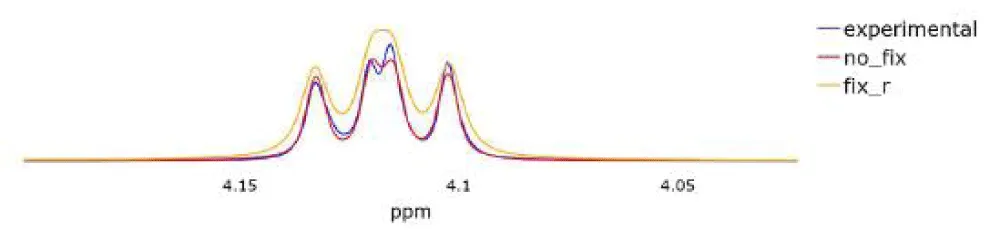
Table 3 represents the metrics for the studied spectra. The first column is responsible for the metric of the model when optimizing all parameters. In other columns, ‘fix J and r’ corresponds to the optimization when we take the initial approximation matrix from [30] and ChenomX as the matrix J. In turn, ‘fix r’ represents optimization without using cor-rection factors⃗r.

For clarity, we will also attach the graphs we have obtained. The graphs in Figure 4 illustrate the experimental spectrum, the spectrum calculated based on the spin system using ChenomX (designated “fix J r”), and the spectrum obtained from a fully optimized Table 3: Comparison of IoU for different spectra of proline model that includes interaction constants and correction factors (designated “no fix”). In Figure 5, it can be seen that the use of relaxation rates significantly improves the accuracy of the spectrum reconstruction. Figure 4 demonstrates how the model effectively handles complex peak features.

Figure 4: Part of the L-Proline NMR spectrum: experimental (blue), fully simulated using our model (red), and simulated with a fixed J matrix from ChenomX and values r = 1 (violet).

Figure 5: Part of the L-Proline NMR spectrum: experimental (blue), fully simulated using our model (red), and simulated with fixed values r = 1 (orange).

Based on the metrics, it can be seen that our model finds the parameters of the spin system more efficiently than the search using the annealing algorithm.

To illustrate how the algorithm works, we tested its performance on molecules of the most common amino acids found in NMR spectra of biological fluids. For this purpose, we uploaded experimental 1H NMR spectra and spin system matrices for these spectra from the GISSMO library. Then we calculated the IoU metric on the experimental spectra for fully optimized systems and on spin system matrices downloaded from GISSMO. The results of the comparison are shown in Table 4.

As can be seen from the table, IoU metrics calculated using our optimized spin-system parameters are more than metrics calculated using J matrices from GISSMO for all studied spectra. Due to the presence of noise, impurities, and asymmetry caused by nonuniformity of the constant magnetic field in the real spectra, all calculated metrics are less than 1. Nevertheless, most of the metrics calculated for optimized parameters are more than 0.9. The lowest IoU value was obtained for the spectrum of glycine, which contains only one peak (see GISSMO); therefore, solving the optimization problem here is generally unnecessary. Thus, our proposed algorithm allows us to effectively optimize the matrices of spin systems and produce better results than manual optimization.

For a further justification of the loss function and metric used, the estimated spectra obtained in the optimization modes indicated above (i.e. ”Full optimization”, ”fix J”, ”Fix J and r”, ”Fix r” like it was used in Table 3) are also compared with the ground-truth data in terms of classic loss functions MSE, MAE, RMSD. The spectrum of the ProlineGISSMO-499.84MHz-bmse000047 metabolite was used for comparison. Table 5 presents the comparison results. It can be seen from the results obtained that optimizing the parameters of the spin system in terms of the selected loss function 6 also improves quality in terms of classical loss functions (which, with precision to the sign, can also be considered as quality metrics in this context). The result obtained justifies the use of the selected loss function.

The obtained data allow us to conclude that our method gives results better than known open-source solutions, while not requiring manual processing. IoU metrics calculated for spin system parameters optimized for five different NMR spectra of L-Proline demonstrate better results than for spin systems with fixed J obtained from [30] and ChenomX. In addition, we demonstrate better optimization of spin system parameters for the spectra of the most common amino acids available in the GISSMO [18] database. The obtained model and parameters of the spin systems of metabolite molecules can be used to automate the determination of metabolite concentrations in biological samples and significantly accelerate and simplify the analysis of samples in the field of NMR metabolomics.

Data availability

The code and associated data used in this study are openly available in the GitHub repository.